Лекция 7
Дифференциальные уравнения
§ Дифференциальные
уравнения 1-го порядка ![]() . Интегральные кривые. Теорема о существовании и
единственности решения с данными начальными условиями (задача Коши)
. Интегральные кривые. Теорема о существовании и
единственности решения с данными начальными условиями (задача Коши)
Дифференциальным уравнением называется уравнение вида ![]() , где
, где ![]() - функция,
определенная в некоторой области
- функция,
определенная в некоторой области ![]() пространства
пространства ![]() ,
, ![]() - независимая
переменная,
- независимая
переменная, ![]() - функция от
- функция от ![]() ,
, ![]() - ее производные.
- ее производные.
Порядком уравнения n называется наивысший из порядков производных ![]() , входящих в уравнение.
, входящих в уравнение.
Функция ![]() называется решением дифференциального уравнения на
промежутке
называется решением дифференциального уравнения на
промежутке ![]() , если для всех
, если для всех ![]() из
из ![]() выполняется равенство:
выполняется равенство:
![]() . Дифференциальному уравнению удовлетворяет бесконечное
множество функций, но при некоторых условиях решение такого уравнения единственное.
. Дифференциальному уравнению удовлетворяет бесконечное
множество функций, но при некоторых условиях решение такого уравнения единственное.
Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
Пример 1. Решить уравнение ![]() . Его решение:
. Его решение: ![]() определено на
определено на ![]() . Отметим, что эта постоянная – произвольная и решение – не
единственное, а имеется бесконечное множество решений.
. Отметим, что эта постоянная – произвольная и решение – не
единственное, а имеется бесконечное множество решений.
|
|
|
Более сложное уравнение, в
котором производная непостоянная, имеет вид: ![]() . Это – уравнение первого порядка, разрешенное относительно
. Это – уравнение первого порядка, разрешенное относительно ![]() . (Термин «разрешенное» означает, что
. (Термин «разрешенное» означает, что ![]() выражается через
остальные величины, в отличие от уравнения общего вида
выражается через
остальные величины, в отличие от уравнения общего вида ![]() , из которого выразить
, из которого выразить ![]() может быть и не
удастся). Это уравнение также имеет бесконечно много решений, отличающихся на
константу C (см. рис.
2):
может быть и не
удастся). Это уравнение также имеет бесконечно много решений, отличающихся на
константу C (см. рис.
2):
![]()
![]() Это решение дифференциального уравнения описывается серией функций:
Это решение дифференциального уравнения описывается серией функций:
при С=0 y=F(x)
при С=1 y=F(x) + 1 и т.д. Таким образом серия графиков получена параллельным переносом на константу С.
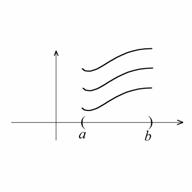 рис.2
рис.2
Более сложные дифференциальные уравнения обычно стараются свести к таким простейшим уравнениям 1-го порядка, разрешенным относительно производной, которые легко решить интегрированием.
Пример 2
Выведем закон движения тела, брошенного с начальной скоростью V под углом α к горизонту.
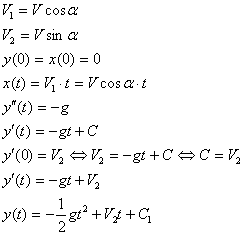
Но по условию y(0) = 0 → C2 = 0 → ![]()
Найдем время подъема: ![]()
Найдем высоту подъема:![]()
Дальность полета xmax (при y(t) = 0
)
y(t) = 0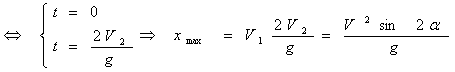
при ![]()
Уравнения, не разрешенные относительно производной. Общее
уравнение первого порядка ![]() можно пытаться решать
разными методами.
можно пытаться решать
разными методами.
Во-первых, можно попытаться
все-таки его разрешить относительно производной
и свести исходное уравнение к одному или нескольким уравнениям вида ![]() .
.
Альтернативные формы записи
такого уравнения: ![]()
![]() .
.
Решение дифференциального уравнения записывают в виде:
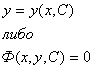 для
неразрешенного относительно производной в виде неявной функции:
для
неразрешенного относительно производной в виде неявной функции:
Пример 3
Решить уравнение ![]() :
: ![]() ,
, ![]() , интегрируя обе части уравнения, получим
, интегрируя обе части уравнения, получим
d(lny) = d(lnx) ![]() .
.
Потенциируя обе части уравнения, получаем общее решение y = Cx, которое изображается серией линейных интегральных кривых, проходящих через точку (0,0). При этом из графика (рис.3) видно, что через любую точку, не принадлежащую (0,0), проходит только одна интегральная кривая (решение).
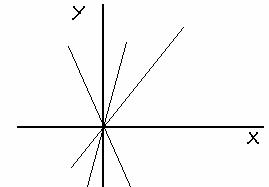
Рис.3
Пример 4
Рассмотрим уравнение
![]() :
: ![]()
![]() интегрируя,
получаем: x2
+ y2
= C = R2 (рис.4)
интегрируя,
получаем: x2
+ y2
= C = R2 (рис.4)
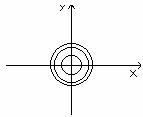 рис.4
рис.4
1) Общее решение– множество решений, содержащее константу.
2) Частное решение получают при подстановке конкретного значения константы в общее решение
Особые решения не входят в общие решения через каждую точку особого решения проходит более одной интегральной кривой.
Пример5
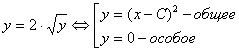 см. рис.5 (через
каждую точку на оси Ох проходит два
решения (две интегральные кривые): частное и особое).
см. рис.5 (через
каждую точку на оси Ох проходит два
решения (две интегральные кривые): частное и особое).
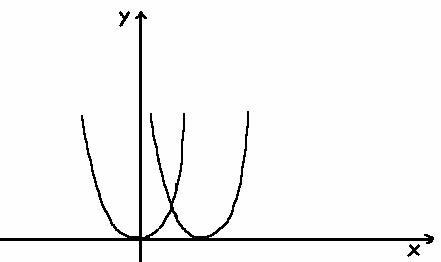
Рис.5
Можно построить интегральную кривую в каждой точке, используя понятие о геометрическом смысле производной: tgα = f(x,y) (рис.6). Таким образом задают поле направлений, т.е. задают прямую в каждой точке, а потом проводят кривую касательную ко всем прямым в этих точках и получают интегральную кривую (одно из решений).
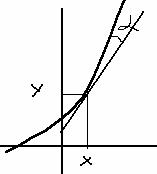 рис.6
рис.6
Сформулируем важнейшую теорему.
Теорема. (О существовании и единственности решения задачи
Коши дифференциального уравнения y’=f(xy) ). Пусть ![]() - непрерывная функция
(рис.7) в области
- непрерывная функция
(рис.7) в области![]() , причем
, причем ![]() - также непрерывна в
- также непрерывна в ![]() . Тогда существует единственное решение y=y(x)
дифференциального уравнения y’=f(xy)
с начальным условием y(x0)=y0, (x0,y0) принадлежит D. Следовательно, через точку
. Тогда существует единственное решение y=y(x)
дифференциального уравнения y’=f(xy)
с начальным условием y(x0)=y0, (x0,y0) принадлежит D. Следовательно, через точку ![]() проходит только одна
интегральная кривая.
проходит только одна
интегральная кривая.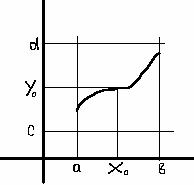
Рис.7
(без доказательства).
Пример 7
Рассмотрим подробнее уравнение ![]() :
:
![]()
![]()
Так как производная функции f(y) неопределена при у = 0 (разрыв вдоль оси Ох), то при у = 0 есть еще одно решение (особое).
Основные тины дифференциальных уравнений
1) Уравнения с разделяющимися переменными. Уравнениями с
разделяющимися переменными называются уравнения вида ![]() , где
, где ![]() - непрерывна на
некотором
- непрерывна на
некотором ![]() , а
, а ![]() непрерывна на
непрерывна на ![]() , причем
, причем ![]() на
на ![]() .
. ![]() (метод разделения
переменных). Интегрируя обе части, получаем
(метод разделения
переменных). Интегрируя обе части, получаем ![]() . Обозначая
. Обозначая ![]() любую первообразную
для
любую первообразную
для ![]() , а
, а ![]() - любую первообразную
для
- любую первообразную
для ![]() , перепишем это уравнение в виде неявно выраженной функции
, перепишем это уравнение в виде неявно выраженной функции ![]() . Это – искомая интегральная кривая.
. Это – искомая интегральная кривая.
Рассмотрим пример такого уравнения
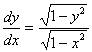
![]() интегрируя,
получим
интегрируя,
получим ![]() . Возьмем синус от обеих частей алгебраического уравнения:
. Возьмем синус от обеих частей алгебраического уравнения: ![]() (общее решение в
неявном виде).
(общее решение в
неявном виде).
2) Однородные уравнения. Под однородными уравнениями понимаются уравнения вида ![]() . Для их решения требуется сделать замену
. Для их решения требуется сделать замену ![]() , после чего получится уравнение с разделяющимися
переменными:
, после чего получится уравнение с разделяющимися
переменными: ![]()
![]()
![]()
![]()
![]() .
.
Уравнения вида 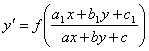 . Такие уравнения сводятся к однородным заменой переменных. В
случае, если прямые
. Такие уравнения сводятся к однородным заменой переменных. В
случае, если прямые ![]() и
и ![]() пересекаются в точке
пересекаются в точке ![]() , то замена
, то замена ![]() приведет уравнение к
однородному. Если же эти прямые не пересекаются, то
приведет уравнение к
однородному. Если же эти прямые не пересекаются, то ![]() и замена
и замена ![]() приведет к уравнению с
разделяющимися переменными.
приведет к уравнению с
разделяющимися переменными.
Рассмотрим параболическое зеркало. Расположим начало координат в фокусе параболы (рис.8). Такое зеркало имеет интересное свойство: при помещении источника света в фокус зеркала лучи, радиально расходящиеся в разные стороны , после отражения становятся параллельными (так получают плоские световые волны), причем по закону отражения угол падения равен углу отражения.
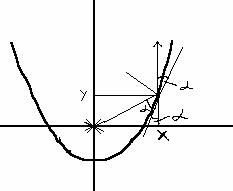 рис.8
рис.8
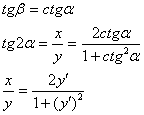
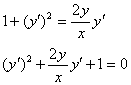
![]()
Введем замену: y = zx ![]() и рассмотрим один
случай, когда
и рассмотрим один
случай, когда![]()
Сокращая на z, получаем ![]() интегрируем
равенство:
интегрируем
равенство:
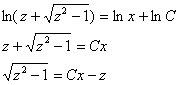
Возводим в квадрат z2 – 1 = C2x2
– 2Cxz + z2 ![]()
Таким образом, получено уравнение
параболы с фокусом в начале координат.
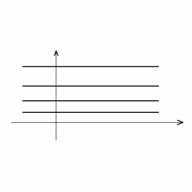 рис.1
рис.1