Лекция 12
Метод неопределенных коэффициентов для нахождения частного решения неоднородного дифференциального уравнения с постоянными коэффициентами.
Представим неоднородное уравнение в виде:
![]() , (1)
, (1)
где P(x) и Q(x) - многочлены, причем ![]() .
.
Частное решение уравнения (1) можно искать в виде:
![]() , где R(x)
и S(x) – многочлены степени m, k –кратность корня
, где R(x)
и S(x) – многочлены степени m, k –кратность корня ![]() характеристического
уравнения
характеристического
уравнения ![]() (k принимается
равным 0, если
(k принимается
равным 0, если ![]() не является корнем
характеристического уравнения).
не является корнем
характеристического уравнения).
Пример. ![]()
![]()
![]()
В данном случае ![]() и частное решение
ищется в виде:
и частное решение
ищется в виде:
![]() ;
; ![]()
Подставляем выражения для ![]() и
и ![]() в исходное уравнение:
в исходное уравнение:
![]()
![]()
![]()
Решение исходного уравнения:
![]()
Решение систем линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим систему
![]() , где
, где 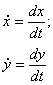
![]() - произвольные постоянные
- произвольные постоянные
Решение представляет собой систему 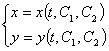 , которая задает линейное векторное пространство R2 .
, которая задает линейное векторное пространство R2 .
Решение системы можно представить также в виде
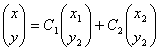 , если
, если 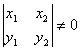 - решения независимы.
- решения независимы.
Исходную систему запишем в виде:
![]() , где A – матрица из коэффициентов
, где A – матрица из коэффициентов ![]() системы.
системы.
Введем невырожденную матрицу B замены
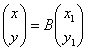
![]()
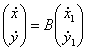
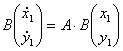
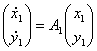 , где
, где ![]()
Матрица A1 запишется в виде 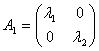 , где
, где ![]() - собственные значения
характеристического многочлена матрицы A (собственные числа):
- собственные значения
характеристического многочлена матрицы A (собственные числа):
![]()
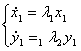
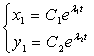
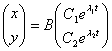 ;
;
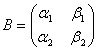 , где
, где ![]() и
и ![]() - собственные векторы
матрицы A.
- собственные векторы
матрицы A.
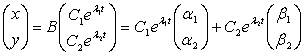
![]()
Пример.
![]()
![]()
Собственные числа матрицы A:
![]()
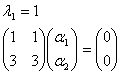 Нетрудно
найти, что
Нетрудно
найти, что ![]()
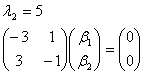
![]()
Общее решение системы уравнений:
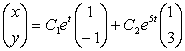
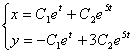
Пример 2. Рассмотрим случай, когда корни характеристического многочлена совпадают.
![]() (1)
(1) ![]()
![]()
![]() , матрица
, матрица ![]() примет вид
примет вид ![]() .
.
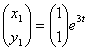 , другое решение нужно искать в виде:
, другое решение нужно искать в виде:
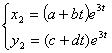 (1’)
, где a,b,c,d – неопределенные коэффициенты.
(1’)
, где a,b,c,d – неопределенные коэффициенты.
Найдем их, продифференцировав уравнения системы (1’) и
подставив выражения для ![]() в уравнение (1)
в уравнение (1)
![]()
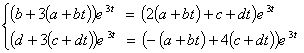
Разделив на ![]() оба уравнения, получим
систему, связывающую неизвестные коэффициенты:
оба уравнения, получим
систему, связывающую неизвестные коэффициенты:
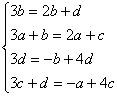 , отсюда
, отсюда ![]() (система вырожденная).
(система вырожденная).
Положим ![]() .
.
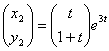 .
.
Проверим систему на линейную зависимость.
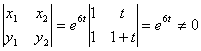
 Таким образом, общий вид решения:
Таким образом, общий вид решения:
![]()
В случае кратных корней одно решение находится сразу, второе – методом неопределенных коэффициентов.
Пример3. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами, имеющих комплексно-сопряженные корни.
![]()
![]()
![]()
![]()
![]()
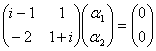
![]()
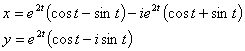
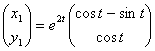
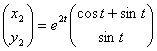
Общее решение:
![]()
Рассмотрим еще один пример, который иллюстрирует решение системы трех линейных дифференциальных уравнений.
Даны две последовательные
химические реакции ![]() и
и ![]() . Скорость каждой из реакций пропорциональна концентрации
реагирующего вещества. Константы скорости реакций равны a и b.
. Скорость каждой из реакций пропорциональна концентрации
реагирующего вещества. Константы скорости реакций равны a и b.
Обозначим x,y,z концентрации веществ A,B и C соответственно.
Система уравнений примет вид:
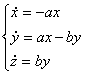
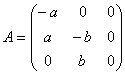
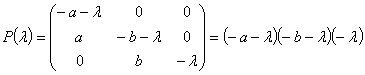
![]()
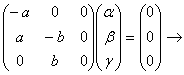 собственный вектор
собственный вектор ![]() .
.
![]()
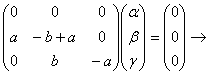 собственный вектор
собственный вектор 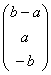 находится из системы
находится из системы ![]() .
.
![]()
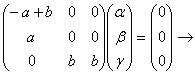 собственный вектор
собственный вектор ![]() .
.
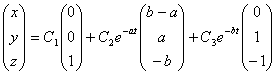
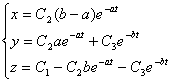
Константы С1,С2 и С3
определяются из начальных концентраций веществ A,B и C.
Лекции
набирали Кузнецова Анна.
Васильев Александр.
Литвинов Юрий.
Селюнин Александр.