25.03.03

Площадь поверхности

Если определять площадь поверхности объемной фигуры по аналогии с плоской поверхностью, как точная нижняя грань суммы площадей граней описанного многогранника, то полученный результат будет неверным. Докажем это:

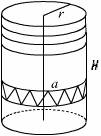Пусть дан цилиндр с радиусом r и высотой h. По известной формуле площадь его боковой поверхности равна:

Найдем теперь площадь цилиндра, как точную нижнюю грань площадь описанного многогранника.

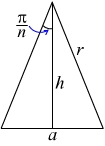
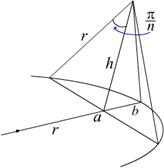Разобьем цилиндр на m дисков, каждый диск – на n треугольников со стороной а (см. рис.). Их суммарная площадь будет равна 2nmS, а площадь цилиндра равна:

Из треугольника на рисунке видно, что

Так как 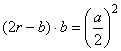, значит, поскольку , получим

и (т.к. ).

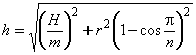и

.

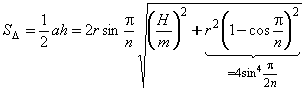Необходимо проверить, что .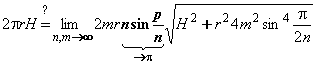

Это равно: 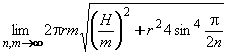. Отсюда получим, выбирая m = n²: 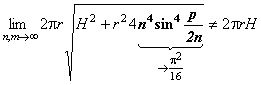. Этот пример называется сапог Шварца.

Поэтому для определения площади используют следующую модель. Пусть:

.

Функция f(x,y) дифференцируема в любой точке из D, следовательно, в любой точке S существует касательная плоскость.

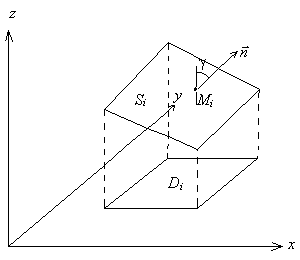
Теперь разобьем компакт D и спроектируем разбиение на S. В i-м элементе разбиения возьмем точку и построим в ней касательную плоскость. Теперь спроектируем i-й элемент D_i компакта D на эту плоскость. Получим плоскую область S_i. Площадь S определяется, как , если существует интегральная сумма T (см. рис.).

– нормальный вектор, n_i – косинусы углов наклона этого вектора к осям координат:

.

Между D_i и S_i существует следующая связь:

где γ – угол наклона нормали к оси z. Отсюда получим:

.

Нормаль имеет следующие координаты:

.

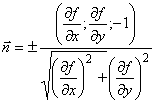± в этом выражении появляется из-за того, что нормаль может иметь два противоположных направления – «вверх» и «вниз», поэтому для определенности рассматриваются двухсторонние поверхности.

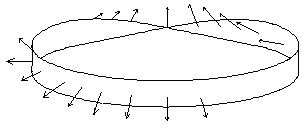
Определение: двухсторонней поверхностью называют такую поверхность, в каждой точке которой нормаль определена однозначно.

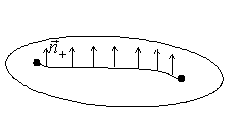При движении по любой кривой на этой поверхности нормаль к поверхности определяется однозначно.

ПРИМЕР:

Односторонняя поверхность – лента Мебиуса:

Для определенности в расчетах будем использовать .

,

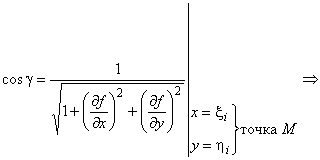
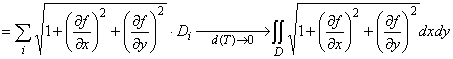
Площадь поверхности, заданной уравнением вычисляется по формуле:

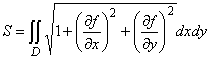(1)

В общем случае, площадь поверхности определяется в параметрическом виде:

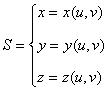
Уравнение нормали.

Обозначим

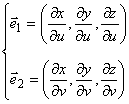
Зафиксируем переменную v. Тогда x, y, z – функции, зависящие от и, и задающие на поверхности S координатную линию. Аналогично, фиксируя u, получим другую координатную линию на поверхности. В результате последовательного фиксирования v и u получим координатную сетку на S.

(2)

Если , то поверхность S – вырождена.

Перепишем уравнение (1), учитывая (2):

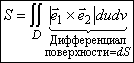
Модуль векторного произведения можно представить так:

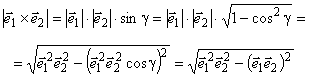
Пусть и . Тогда уравнения для и будут выглядеть так:

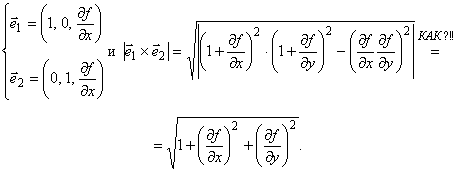
ПРИМЕРЫ:

1) Площадь боковой поверхности цилиндра.

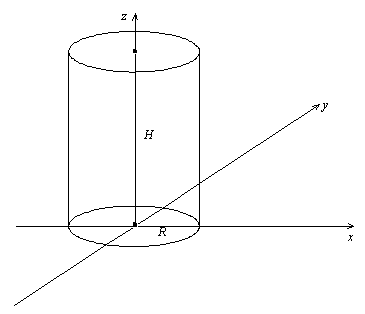
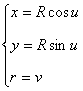
и

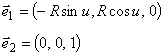
Тогда:

.

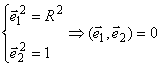
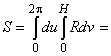
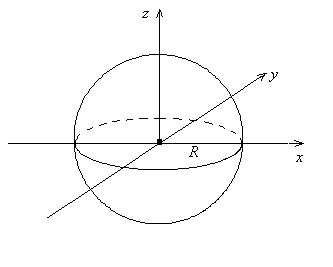2) Площадь сферы.

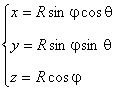, где

,

, поэтому

.

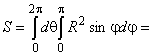
Поверхностные интегралы

Поверхностные интегралы первого рода:

.

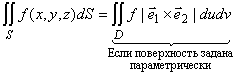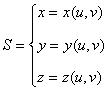– невырожденная поверхность.

Если .

Поверхностные интегралы второго рода:

Пусть есть вектор функция . Выберем положительную нормаль:

, тогда

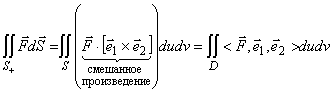, где

.

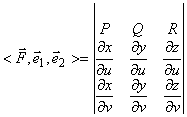Если S такова, что , тогда:

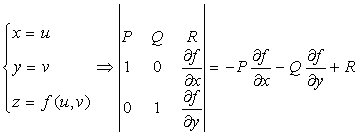. Таким образом, получаем:

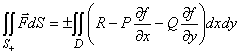
ПРИМЕР:

.

Уравнение поверхности сферы: . Зададим сферические координаты:

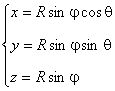. Тогда

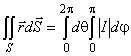, где

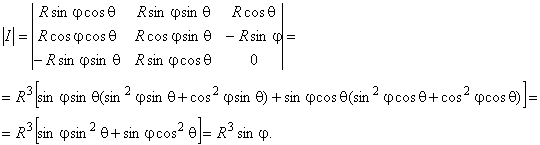
Следовательно, поверхностный интеграл запишется, как:

.
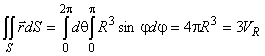