15.04.03

Потенциальные, соленоидальные и

гармонические поля

1. Потенциальное поле

Пусть есть две точки А и В.

Пусть – поле.

Поле называется потенциальным, если выполняется одно из условий:

1)

2) . Если это выполнено, то U называется потенциалом поля.

, где – гравитационное поле является потенциальным: .

Поле называется центральным, если Отсюда следует, что потенциально:

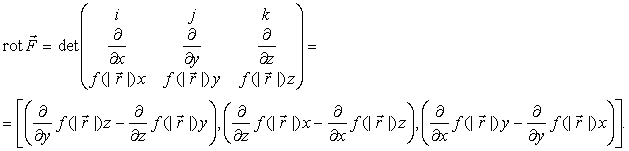
При этом, . Следовательно, и выполняется первое из условий потенциальности поля. Поэтому любое поле вида – потенциальное, значит, можно найти его потенциал.

Рассмотрим функцию . Докажем, что:

. Аналогично получим, что и . Следовательно, всякое центральное поле – потенциально.

2. Соленоидальное поле

Поле – соленоидальное, если его дивергенция равна нулю:

.

По формуле Гаусса–Остроградского:

Поток соленоидального поля через любую поверхность равен нулю. Соленоидальные поля характерны для движения потоков жидкостей и газов.

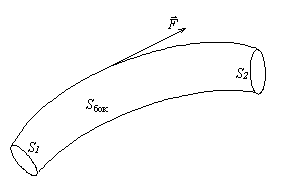Поток через боковую поверхность S_бок всегда равен нулю, так как направлен по касательной к этой поверхности.

Поток через S₁ равен потоку через S₂ с обратным знаком – «сколько вошло, столько вышло».

Утверждение: Если поле – соленоидальное, то оно является ротором поля , то есть если , то , где – векторный потенциал. Поэтому . Докажем это:

.

,

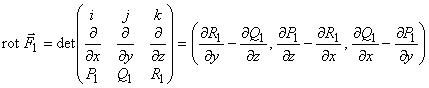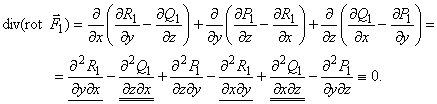
Докажем также, что:

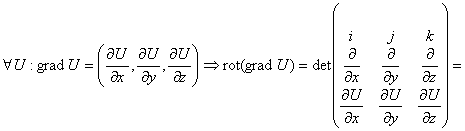
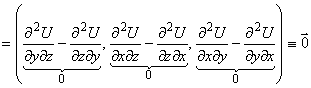. Доказано.

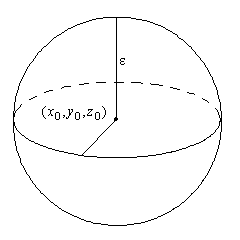
Рассчитаем площадь поверхности сферы:

Пусть дана сфера радиуса ε с центром в точке .

Пол теореме о среднем:

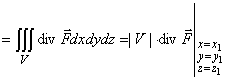
Перейдем к пределу:

.

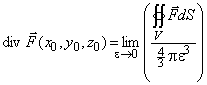Это выражение можно рассматривать, как определение дивергенции. Из него видно, что дивергенция не зависит от системы координат, в которых решается задача.

Дивергенция – это интенсивность потока поля. Аналогично, ротор – завихренность поля . В некоторых учебниках ротор называется вихрь.

Ротор является инвариантом относительно системы координат.

3. Гармоническое поле

Гармоническим называется поле, для которого и ротор и дивергенция равны нулю.

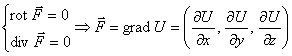и

.

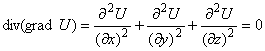Это выражение – уравнение Лапласа. Его решением является гармоническая

функция, поэтому поле, обладающее такими свойствами, называется гармоническим.

ПРИМЕР:

В качестве примера рассмотрим гравитационное поле, которое является единственным центральным полем, одновременно имеющим свойства гармонического.

Докажем, что всякое центральное гармоническое поле – гравитационное и наоборот.

1. . Это условие проверено выше.

2. . Используем это условие:

. Пусть , тогда.

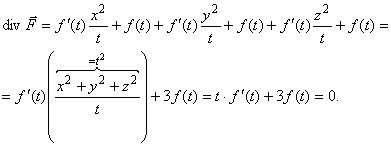
Отсюда получаем:

. Интегрируя обе части по t, получим:

,

. Отсюда, возвращаясь к , получим, что . Следовательно, так как , окончательно получаем, что , а это по определению – гравитационное поле.