Статистические аналоги термодинамических функций

Мы уже получили соотношение статистического среднего для любой функции динамических переменных системы F Показали также, что для равновесных систем при рассмотрении методами классической механики можем задать функцию распределения

В общем случае для системы с дискретными уровнями энергии Тогда получаем соотношения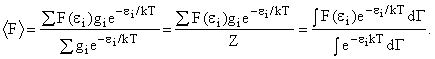

Расположение уровней энергии зависит от объема и внешних воздействий. Сумма по состояниям также зависит как от объема, температуры, так и от внешних воздействий. Если мы умеем расчитать Z, то можем вычислить среднее значение функции. Здесь пользуются следующим приемом. Пусть Z непрерывная функция некоторого параметра х. То очевидно Сравнив с предыдущим увидим, что dlnZ/dx имеет смысл среднего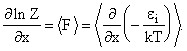

Как постулат примем, что определенные таким образом функции тождественны тер-модинамическим и внутренняя энергия U тождественна средней энергии системы при постоянном объеме с точностью до U_o - энергии системы при абсолютном нуле.

U = U_o + <e>. Из предыдущего уравнения видно, что можем выразить через lnZ.

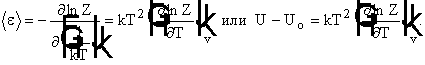Теперь все делается просто. Поскольку приняли постулат о тождестве статистических средних и термодинамичес-ких функций, то все остальные функции получаем из этого фундаментального уравне-ния связи.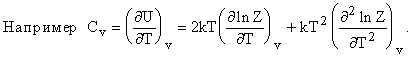

Для свободной энергии Гельмгольца F просто можно получить Вспомнив выражение для U, видим , т.е. F/ T можно положить равной ( - k lnZ), но при этом надо учесть, что это с точностью до неопределенной функции от объема. Из классической термодинамики на основании третьего закона знаем, что при абсолютном нуле U и F равны U_o. Тогда получаем F = U_o - kTlnZ. Отсюда легко получить энтропию и давление

Теперь получим выражения для H и G.

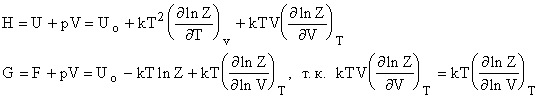
Можно получить и химический потенциал .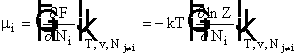

Итак, для расчета термодинамических функций надо уметь считать Z. Причем не всегда само значение Z. Так для расчета энергии и теплоемкости достаточно знать Z как f(T), для расчета давления - Z как f(V).

Итак статистическая сумма по состояниям

- безразмерная характеристическая функция,

- значение суммы не зависит от состава ансамбля, M ® ¥ , а определяется природой системы (модель задает энергию и g_i, число молекул, Т, V, природу внешних сил, влияющих на энергию и g_i).

- геометрический образ суммы: объем фазового пространства, определяющий число доступных состояний, задаваемых функцией распределения в Г - пространстве. Это следует из способа задания суммы Многомерный интеграл определяет эти свойства суммы, дает объем фазового пространства, а объем фазового пространства определяет число микросостояний системы.

- cумма по состояниям введена как нормировочный множитель для dW(p, q) - вероятности того, что случайно выбранная система попадет в бесконечно малую область dГ в окрестности точки фазового пространства с координатами p, q при переходе от

r(p, q) к r(e). Введение этого множителя упрощает вычисление средних для функций ансамбля. Операция сводится в вычислениям lnZ и дифференцированию lnZ.

Теперь докажем равенство b = 1/ kT и определим a. Обозначим b = 1/ q. Рассмотрим далее некоторые свойства функции lnP, которую мы использовали при выводе распределений. Эта функция аддитивна, при мысленном разбиении объема системы на части число способов распределения всех элементов по энергетическим ящикам равно произведению числа способов для каждой части. Математически это мультипликативная функция и ее логарифм аддитивен. В классической термодинамике такими свойствами обладает энтропия. Она растет в изолированной системе и имеет максимум в равновесии. В статистике в равновесии будет максимум lnP. Отсюда следует постулат Больцмана: S = k lnP. Для упрощения часто пользуются безразмерной величиной S = S/ k.

Рассмотрим для примера бозоны. Для них имели соотношения.

Найдем безразмерную энтропию

Эта формула общая для равновесного и неравновесного состояний.

Из выведенных ранее соотношений следуют очевидные равенства

Подставим эти соотношения в выражение для энтропии и получим

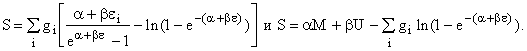
Эта формула относится к равновесному состоянию, поскольку использовали равновесную фукцию распределения.

Будем рассматривать систему в отсутствии внешних полей и при постоянном V, т.е. можно считать e_i, g_i и V постоянными. Тогда продифференцировав по a и b, получим

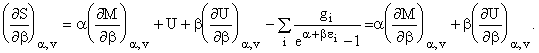
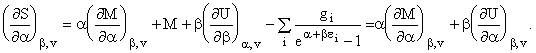
Домножив уравнения на da и db соответственно и сложив, получим . Из феноменологической термодинамики известно: Получаем

a = - m/ T и b = 1/ T, а т.к. использовали S/ k, то в общем случае a = - m / kT и b = 1/ kT.