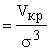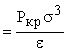Бинарная [n⁽²⁾(r₁₂)] или радиальная (Дебая-Менке) [g(r₁₂)]

функции распределения.

Если имеем N частиц и образуется группа из 2 (s в общем случае) частиц, другая группа из N - 2 (или s) частиц находится в поле группы 2 или s, то может быть введена функция распределения. Если использовать модель парных взаимодействий, то вероятность образования парной конфигурации определяется бинарной функцией плотности вероятности: . В общем случае вместо 2 будет s. Если в группах по 1 частице, то имеем функцию n⁽²⁾(r₁r₂) для описания их расположения. Для 1 частицы n⁽¹⁾ просто плотность n, для 2-х частиц n⁽²⁾(r₂/r₁)/ n - плотность частиц второго сорта на расстоянии r от первой, а g(r₁₂) = n⁽²⁾(r₂/r₁)/ n² - нормированная безразмерная радиальная функция

При этом полагают, что полная энергия равна сумме потенциальных энергий пар молекул - межмолекулярные силы аддитивны, т.е. присутствие других молекул не влияет на энергию взаимодействия пары, потенциал взаимодействия не зависит от угла и применима классическая механика. Очевидно неприменима для молекул, имеющих дипольный момент, т.е. где энергия зависит от расположения атомов.

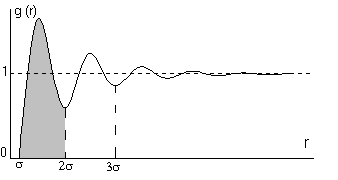
В твердом теле такая функция - вертикальные линии на расстояниях, соответствующих параметрам кристалла (расстояниям в первой, второй и т.д. координационных сферах). В жидкости будут размытые экстремумы.

Рассмотрим как получаются формулы для функций распределения. Вероятность обнаружить частицу в элементе объема для изотропной среды при хаотическом расположении частиц: dw_х = dv/ V = 4pr²dr/ V. Если есть упорядоченность, корреляции - предел в кристалле, то учитываем это функцией g(r) - радиальной функцией распределения.Тогда вероятность dw_к = g(r)dv/V = g(r)4pr²dr/ V. При отсутствии взаимодействия (хаосе) очевидно, что g(r₁₂) = 1.

Точно расчитать функцию g для любого потенциала межмолекулярного взаимодействия трудно, в некоторых приближениях - по Кирквуду-Боголюбову. Цепочки Боголюбова-Борна-Грина-Кирквуда-Ивона: если присутствует внешний потенциал u(r) и энергия парного взаимодействия u(r_i, r_j), то в общем случае для для группы из s частиц функция распределения: 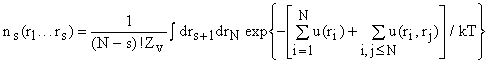. Применяя операцию градиента и умножая на - kT, получаем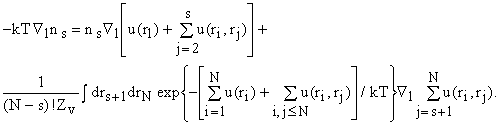

Каждое из слагаемых N - s справа дает одинаковый вклад в интеграл и можем упростить: 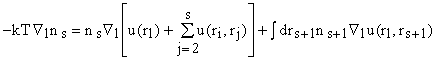, где s = 1,2 ... Уравнения для n_s при разных s дают последовательность зацепляющихся друг за друга уравнений - цепочка Боголюбова.

Обычно вид функции g находят по данным рассеяния электрона или рентгеновских лучей. Функция быстро затухает (в твердых телах она периодична) и вводят радиус корреляции r, при котором g(r) (в пределах заданной точности) » 1, обычно

r » 3s ( s - параметр потенциала 6 - 12).

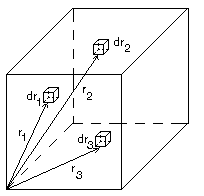
Введем теперь фунцию dn(r). Вероятность нахождения двух выбранных частиц в элементах объема dv₁ и dv₂ и в точках на концах векторов r₁ и r₂:

dw(r₁₂) = [dv₁dv₂/ V²] g(r₁₂). Число произвольных частиц, находящихся на расстоянии r от выбранной, найдем умножением dw(r₁₂) на N(N-1) » N² и интегрированием по координатам первой частицы по всем ориентациям вектора r₁₂. Число частиц на расстоянии r и в объеме V равно

Число пар молекул, находящихся на расстоянии r в интервале r ® r + dr тогда: .

С другой стороны бинарная функция распределения: определяется из условия: вероятность обнаружить одну частицу в элементе объема dr₁ около r₁, а другую в элементе объема dr₂ около r₂ равна

. U_N - энергия взаимодействия N частиц. В макросистеме эта функция зависит только от r₁ и r₂.

Число молекул в непосредственном окружении выбранной молекулы c (координационное число). Оно по смыслу отличается от координационного числа в твердом теле - там оно строго заданная и постоянная (кроме поверхности) величина. В жидкости это некое среднее, поэтому может быть не целым числом и зависит от температуры (меняется плотность жидкости). Из заданной модели его легко посчитать как число молекул в слое от s до 2s. Получим 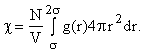Теперь, зная dn(r), можно считать переменные, определяющие термодинамические свойства, зависящие от расстояния между частицами. Например, средняя энергия взаимодействия частицы и суммарная энергия

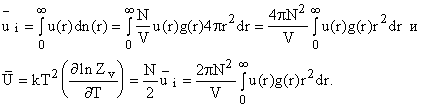
Расчет составляющих внутренней энергии, зависящих от поступательного, колебательного и вращательного движений, расчитывается независимо от межмолекулярного потенциала. Для вывода уравнения состояния надо решить уравнение для чего удобно ввести новые декартовы координаты:

x _i' = x _i / V ^1/3. Тогда элемент объема конфигурационного пространства

dv₁...dv_N = V^N dx₁'...dz_N', а сам конфигурационный интеграл равен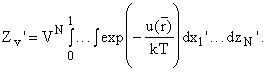

И давление будет определяться как

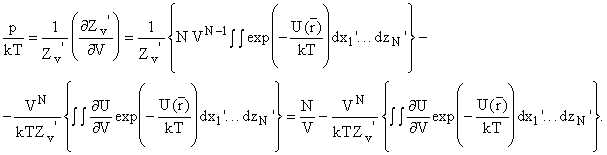
В первом члене сократили конфигурационный интеграл. Для расчета надо еще выразить производную полной энергии U по объему. Если энергия парных взаимодействий аддитивна и U - сумма u парных взаимодействий, то можно определить нужную производную 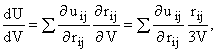т.к. из геометрии следует что Это легко показать: r_ij = [(x_i-x_j)² +...]^1/2 = V^1/3[(x_i'-x_j')² +...]^1/2, т.е.

dr_ij/ dV = (1/ 3)V^2/3[(x_i'-x_j')² + ...]^1/2 = r_ij/ 3V. Тогда

pV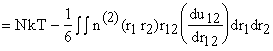. Вспомним: n⁽²⁾(r₁₂) = [N(N-1)/V²]g(r₁₂).

1/ 6 получается из рассмотрения объема, u₁₂ - потенциальная энергия взаимодействия пары молекул (вириал) или 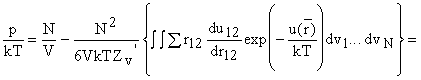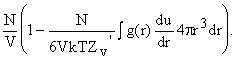Здесь N²/ 2 слагаемых.

Другой способ: По теореме вириала средняя полная кинетическая энергия молекул равна величине вириала , где F - средние силы, r - средние расстояния. Уравнение состояния по теореме вириала можно записать в виде

. Функцию g здесь можно разложить в ряд по плотности частиц в единице объема Получаем аналогию с вириальными уравнениями.

Для разреженных газов 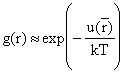и переходим к уравнению состояния со вторым вириальным коэффициентом 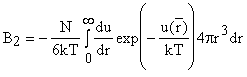. Совпадение с уравнением Майера.

Здесь в формуле для функции распределения берем только первый член:

Если взять функцию распределения для жидкости, получим уравнение состояния для конденсированной фазы.

Cопоставление оценки приведенных значений с использованием функции распределения с данными опыта и расчетом по теории свободного объема:

	функция распределения	теория свобод-ного объема	опыт для нулевой группы
Т* кр	1,433	1,30	1,26
V* кр	2,585	1,77	3,15
Р* кр	0,199	0,434	0,117
z; - фактор сжимаемости	0,358	0,591	0,293

Расчет проведен при использовании упрощенного потенциала Леннард-Джонса (при r < s принимаем u(r) = + ¥). Довольно значительное различие связано с нестрогим заданием потенциала взаимодействия.

Из допущений самого вывода следует, что следует ожидать совпадений опыта и расчета для простых молекул, близких к сфере и не имеющих дипольного момента: для благородных газов в первую очередь.

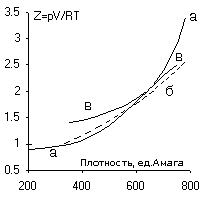
На нижнем рисунке приведены экспериментальные данные (а) при 273 К для фактора сжимаемости аргона, б - расчет с использованием радиальной функции (пунктир), в - расчет по методу ячеек.

Плотность в системе Amagat: Принимается как стандартное состояние 1 атм, 0^оС, объем моля 22,4 л. Для идеального газа это 44,616 моля / м³. Единица плотности M/ V_m. Для аргона (M = 39, 95) при 273 К: 200 ед. Амага = 0,3568, 400 = 0,7136, 600 = 1,070 г / см³.

Для растворов надо учитывать три радиальные функции: g₁₁(r), g₂₂(r), g₁₂(r) = g₂₁(r) и учесть вклады соответствующих частиц: 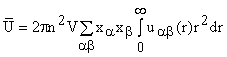. n - общее число молекул, x_a - мольная доля вещества А, u_ab - потенциал взаимодействия частиц двух типов.

Строго задачу статистического рассмотрения жидкости можно решить, зная межмолекулярный потенциал, но это пока невозможно. Успешнее решается задача определения термодинамических свойств жидкости по данным по строению молекул и их расположению в жидкости. Методы Монте-Карло и молекулярной механики.

Метод Монте-Карло: использование при расчете случайных чисел с заданным законом распределения. Расчитывается конфигурационный интеграл для определенного потенциала взаимдодействия. В методе молекулярной динамики решаются уравнения движения. Экспериментальное моделирование: встряхивание твердых шаров в емкостях с нергулярно шероховатой поверхностью.